Hsin-Po's Website

Distributed Storage Papers

The following are my works on distributed storage systems. They study regenerating codes.

• [MoulinAlg21] I. Duursma, H.-P. Wang. Multilinear Algebra for Distributed Storage. SIAM Journal on Applied Algebra and Geometry (SIAGA).
• [Atrahasis21] I. Duursma, X. Li, H.-P. Wang. Multilinear Algebra for Minimum Storage Regenerating Codes: A Generalization of Product-Matrix Construction. Applicable Algebra in Engineering, Communication and Computing (AAECC).

A regenerating code consists of

• a file of size $M$ symbols and
• a system of $n$ storage devices, called nodes.

The configuration of the nodes satisfies the following conditions:

• Each node stores $\alpha$ symbols of the file.
• Any $k$ nodes contains sufficient information to recover the file.
• When a node fails, some $d$ other nodes will each send it $\beta$ symbols to repair the failing node.

The code is named regenerating mainly due to the last bullet point—the nodes regenerate themselves.

The theory of regenerating codes concerns the relation among $n,k,d,\alpha ,\beta ,M$. For example, since any $k$ nodes contain $k\alpha$ symbols and can recover the file, the file size $M$ is at most $k\alpha$. Similarly, since $d\beta$ symbols repair a failing node, the node size $\alpha$ is at most $d\beta$. (Exercise) One can also show that $k-1$ nodes ($\alpha$) plus $d-k+1$ help messages ($\beta$) is at least $M$. There is a family of bounds of this type. They are called cut-set bounds and restrict where those parameters can live.

The opposite approach is to construct regenerating codes that aim to achieve low $\alpha$, low $\beta$, and high $M$. [MoulinAlg21] utilizes multilinear algebra to do this. We construct a series of regenerating codes which we call Moulin codes. They achieve the best known $\alpha /M$-versus-$\beta /M$ trade-off to date. And it is conjectured that this trade-off is optimal.

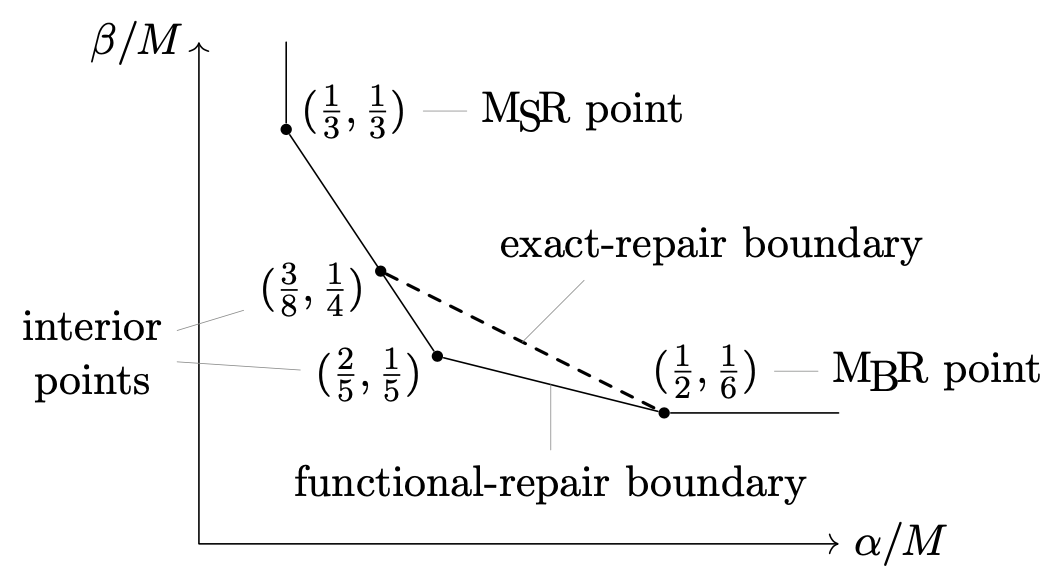
Here is a plot detailing the $\alpha /M$-versus-$\beta /M$ trade-off for the $(n,3,3)$ case.

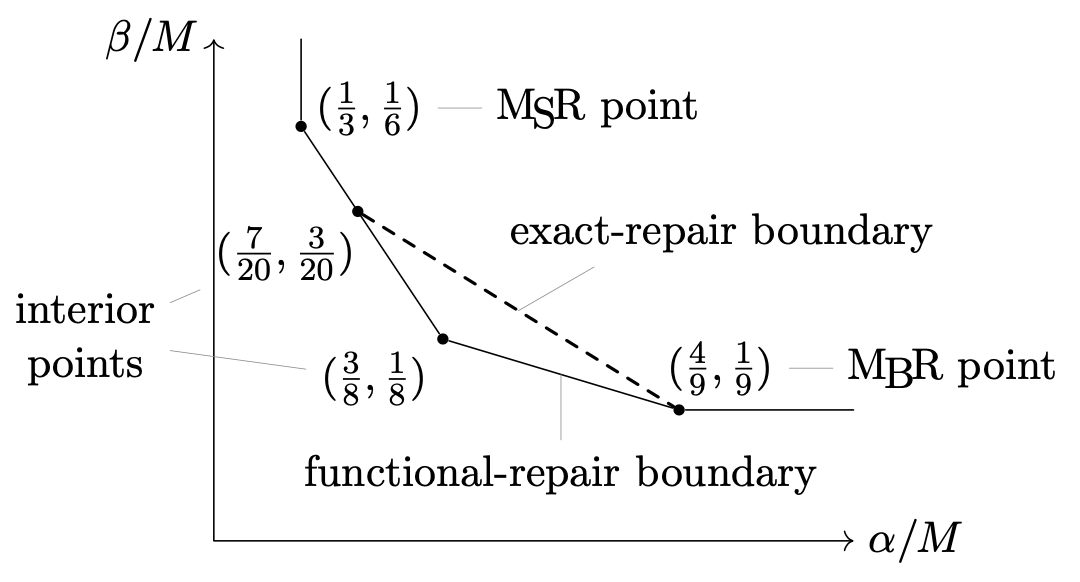
Here is another $\alpha /M$-versus-$\beta /M$ trade-off for the $(n,3,4)$ case.

For more general parameters, check out this D3.js plot.

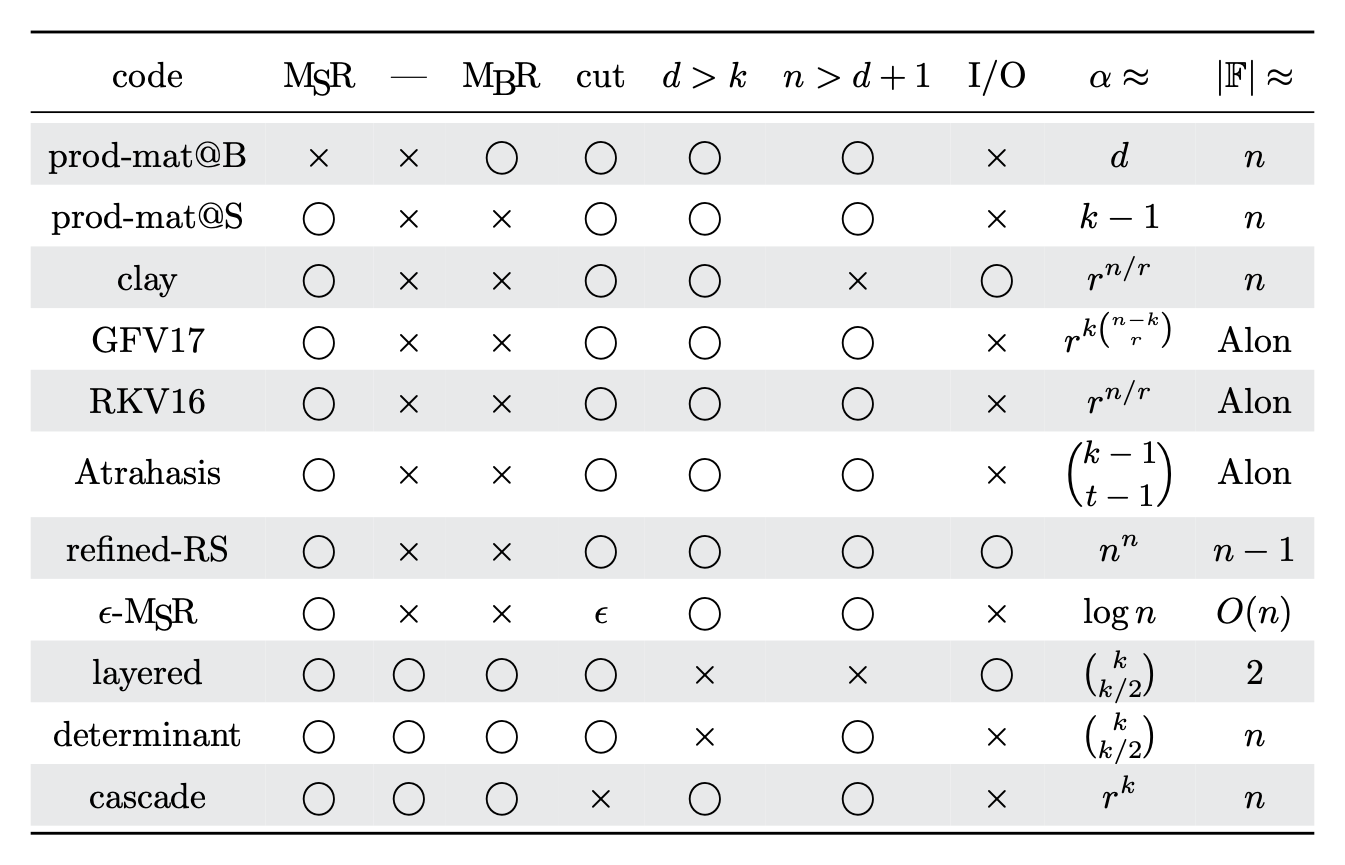
See also thus table for the relations among some competitive constructions.

The construction of MoulinAlg21 makes use of tensors and wedge powers. These spaces are arranged is a clever way so the data recovery can be done in a sequential manner.

[Atrahasis21] exploits multilinear algebra to construct MSR codes, which we called Atrahasis codes. Formally, an MSR code is a regenerating code with $M=k\alpha$ and $\beta = \alpha/(d

• k + 1)$.Fromtheconstrainton$M$ one sees that there is no wastes of storage (hence the name minimum storage regeneration = MSR). Some researchers see MSR codes as the intersection of regenerating codes and MDS codes.

MSR alone attracts significant attentions because people want to minimize node size ($\alpha \ge M/k$), and only then they minimize help messages ($\beta \ge \alpha /(d-k+1)$ given that $\alpha \ge M/k$). Here is a table for a comparison of some existing contraptions.